Gauss Elimináció

Vektorok (előismeret)

• Független vektorok:
  • 2 vektor esetén: amennyiben nem párhuzamosak,
  • 3 vektor esetén: amennyiben nem egysíkúak,
  • 4 vektor esetén: amennyiben nem egyhipersíkúak.
• Összefüggő vektorok: amennyiben nem függetlenek.
  • Ha több sor van mint oszlop.

Gauss-Jordan Elimináció [^1]

Egyenletrendszer megoldása mátrix alakú felírása alapján.

Fontos

Sorokat nem cserélhetünk fel, oszlopokat igen.

Mátrix számológép (Gauss elimináció megoldásához)

Vezérelem [^2]

Minden sorban és oszlopban kiválaszthatunk egy (nem nulla) számot.

Rang [^2]

[[#Vezérelem [ 2]|Vezérelem]]ek száma a megoldásvektoron kívűl, az együttható ($A$) oldaláról.

• Ez adja meg a képtér dimenzióját
• jele: $\text{rang}(A)$

Bővített mátrix rangja

A [[#Vezérelem [ 2]|vezérelem]]ekek száma mindkét, az együttható oldaláról és a megoldásvektor oldaláról is.

• Jele: $\text{rang}(A|b)$

Szabadsági fok [^4]

Más néven a magtér dimenziója. A szabad változók ([[#vezérelem [ 2]|vezérelem]]mel nem rendelkező oszlopok) száma.

Nullsor [^3]

Olyan sor a mátrixban, ahol minden szám nulla. (még a megoldáshalmazban is).

Info

Ha azonos az oszlopok száma és a sorok száma azonos, jelentése: voltak benne összefüggő vektorok.

Tilos sor [^4]

Olyan sor ahol az együttható oldalán ($A$) csak nullák vannak, míg a megoldáshalmaz ($b$) nem nulla.

Info

Jelentése: nem lesz megoldása az egyenletrendszernek.

Homogén egyenletrendszer

Ha a megoldásvektor ($b$) nulla, homogén egyenletrendszerről beszélünk.

Info

Jelentése: mindig lesz legalább egy megoldása. Ez a triviális megoldás, a nulla.

Inhomogén egyenletrendszer

Inhomogén egyenletrendszerről beszélünk ha nem homogén, vagyis ha a megoldásvektor ($b$) nem nulla.

Feladatok

• Lineáris Algebra Feladatgyűjtemény 7. oldal.
• 01-02 Gyakorlat feladatsor
• 03 Gyakorlat feladatsor
• 04-05 Gyakorlat feladatsor
• Gauss Elimináció

Megoldások

• 01-02 Gyakorlat feladatsor megoldás
• 03 Gyakorlat feladatsor megoldás
• 04-05 Gyakorlat feladatsor megoldás

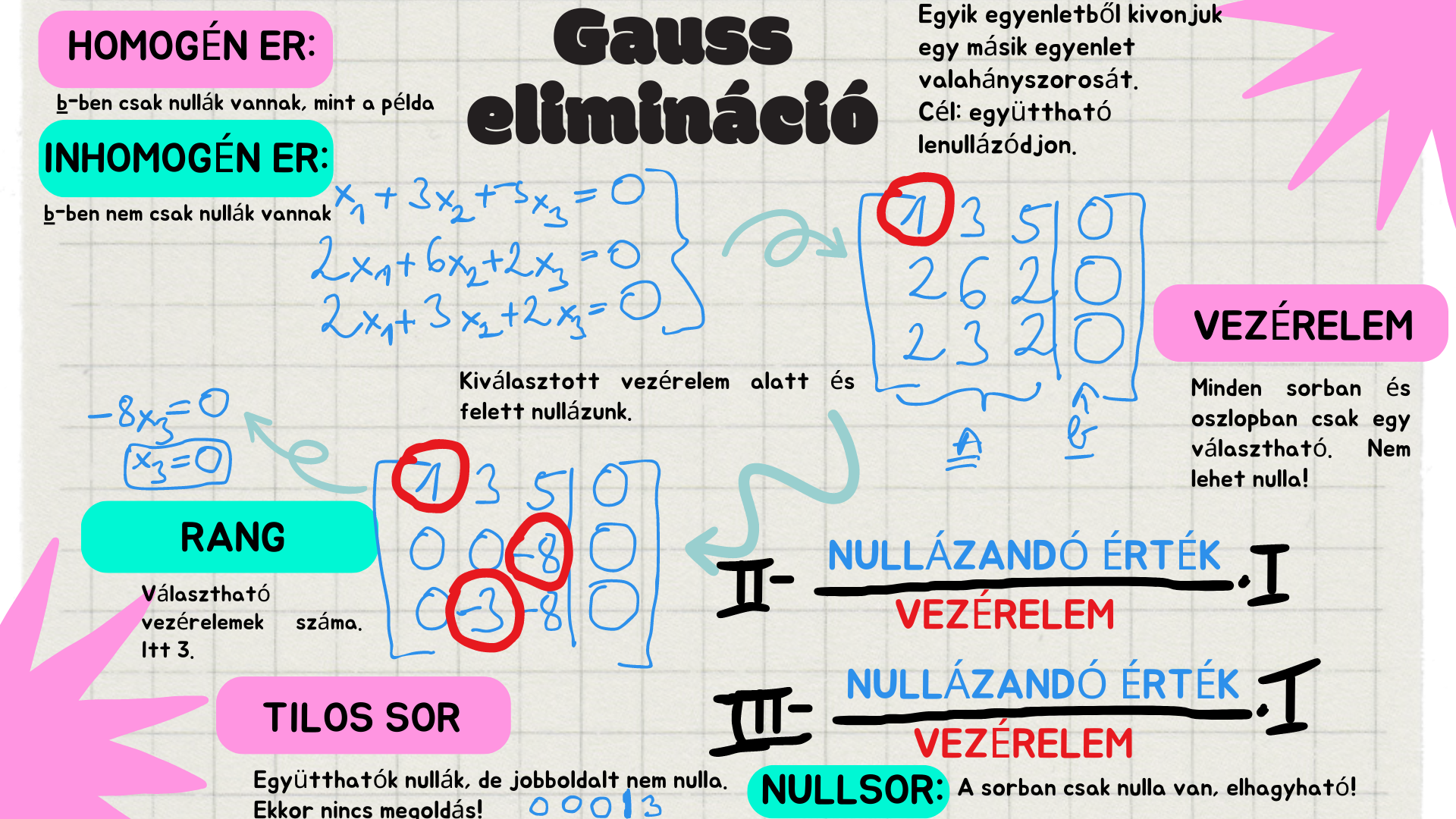|Miski Marcell féle infografika. |Miski Marcell féle infografika. |Miski Marcell féle infografika.

---

[^1] Lineáris Algebra Tankönyv 11. oldal [^2] Lineáris Algebra Tankönyv 12 [^3] Lineáris Algebra Tankönyv 15. oldal [^4] Lineáris Algebra Tankönyv 16. oldal