13 - Végtelen összeg

Számsor (Sor) ¹

Számsor alatt adott $(a_n)\in \mathbb{R}$ számsorozat összegét értjük a végtelenben. $(\sum a_n)$

Fontos

A számsor nem azonos a számsorozattal!

Konvergens ²

1. Az $({\sum }_{n=0}^{\infty }{a}_n)$ sor konvergens, ha a rész-sorozatai ($s_n={\sum }_{k=1}^n{a}_k$) konvergensek.
2. Ha $\exists {\lim }_{n\to \infty }{s}_n=s$. Ekkor a sor összege: ${\sum }_{n=1}^{\infty }{a}_n=s$

Divergens ³

Nincs megoldása.

Számsor $n$-dik részletösszege

$s_n={\sum }_{k=1}^n{a}_k$

Mértani sor ²

A ${\sum }_{n=1}^{\infty }{q}^{n-1}$ [[#Számsor (Sor) [ 1|számsor]] elnevezése mértani sor. $q\in \mathbb{R}\backslash \{0\}n\in \mathbb{N}$ ${\sum }_{n=1}^{\infty }{q}^{n-1}$

Mértani sor, $q\ne 1$

$s_n=1+q+q^2+\dots +q^{n-1}=\frac{1-q^n}{1-q}$ Ezért: ${\lim }_{n\to \infty }{s}_n=\frac{1}{1-q}\text{ha}|q|<1$ ${\lim }_{n\to \infty }{s}_n=\infty \text{ha}q\ge 1$ ${\lim }_{n\to \infty }{s}_n=\beta \text{ha}q\le -1$ Ezért: A mértani sor, ha $q\ne 1$ divergens.

Mértani sor, $q=1$

$s_n=1_1+1_2+\dots +1_n=n$ Ezért: ${\lim }_{n\to \infty }{s}_n=n$ Ezért: A mértani sor, ha $q=1$ konvergens.

Nullsorozat ⁴

• Ha $(\sum a_n)$ [[#Konvergens [ 2|konvergens]], akkor $(a_n)$ nullsorozat.
• $(a_n)$ nullsorozat, ha határértéke $0$.

Divergencia teszt ⁵

Ha $(a_n)$ nem [[#Nullsorozat [ 4|nullsorozat]], akkor$(\sum a_n)$ [[#Divergens [ 3|divergens]].

Info

Az állítás megfordítása nem igaz. Ha $(a_n)$ [[#Nullsorozat [ 4|nullsorozat]], akkor $\sum a_n$ lehet [[#Divergens [ 3|divergens]] is.

Cauchy feltétel

Az $(a_n)$ sorozat eleget tesz a Cauchy feltételnek, ha $\forall \epsilon >0$-hoz van olyan $N$ küszöbindex, $N=N(\epsilon )$, melyre teljesül, hogy: $|a_n-a_m|<ϵ\forall n,m\ge N.$

Cauchy sorozat ⁶

Az $(a_n)$ sorozat Cauchy sorozat, ha eleget tesz a Cauchy feltételnek.

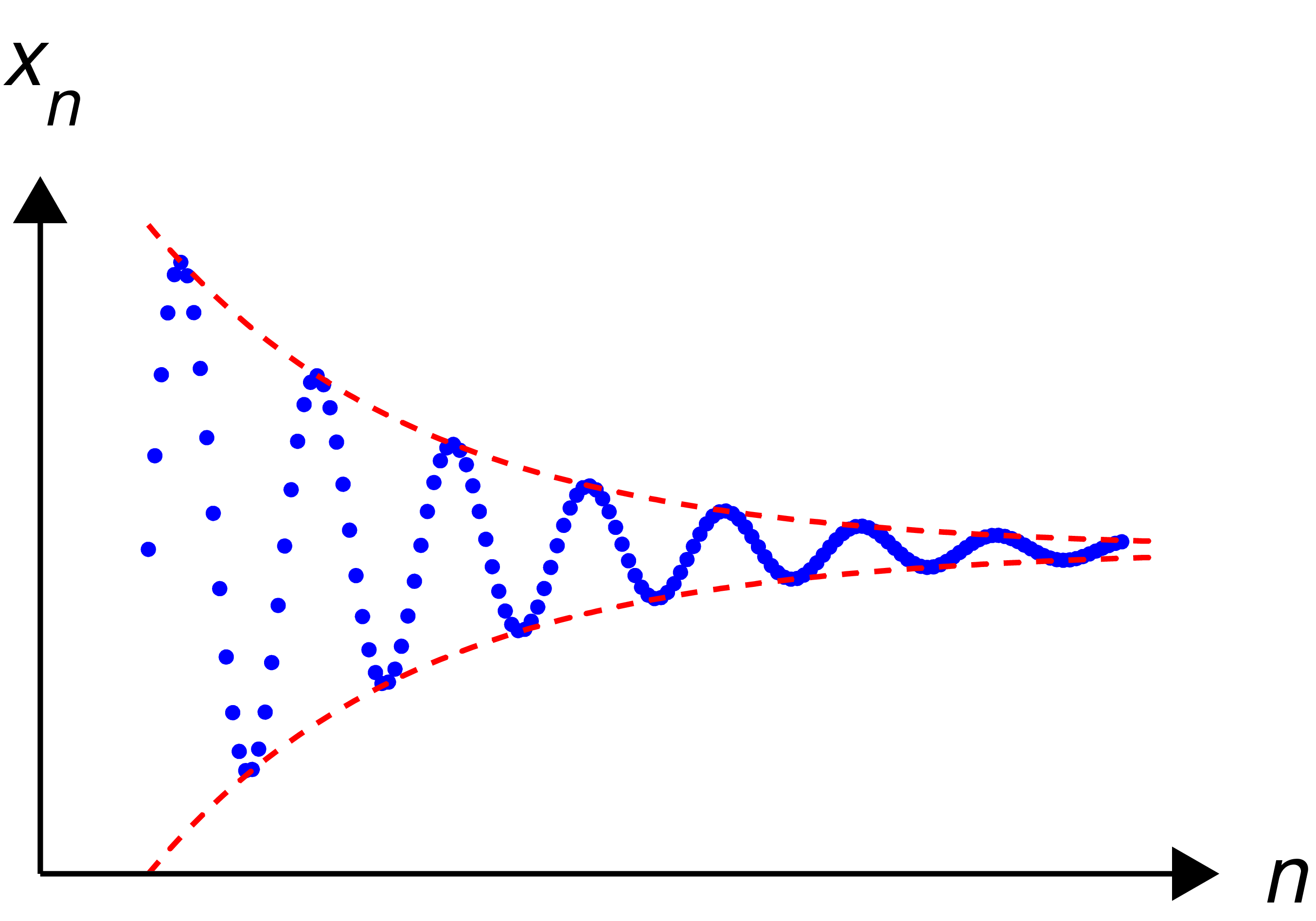
Cauchy sorozat kapcsolata a [[#Konvergens [ 2|konvergenciával]]⁶

Tétel

Egy $(a_n)$ sorozat pontosan akkor konvergens, ha Cauchy sorozat.

Bizonyítás

Az egyik irányt igazoljuk. Tegyük fel, hogy $(a_n)$ konvergens: ${\lim }_{n\to \infty }{a}_n=A.$ Minden $\epsilon >0$ mellett az $\epsilon /2$ számhoz $\exists N$ küszöbindex, melyre $\forall n,m\ge N$ esetén $|a_n-A|<\frac{\epsilon }{2}.$ Ekkor a háromszög egyenlőtlenség miatt $|a_n-a_m|=|(a_n-A)+(A-a_m)|\le |a_n-A|+|a_m-A|\le \frac{\epsilon }{2}+\frac{\epsilon }{2}=\epsilon$

Példa

$a_n={\sum }_{k=1}^n\frac{1}{k}$ Becsüljük meg az $n$-edik és a $2n$-edik tag különbségét. $a_{2n}-a_n={\sum }_{k=n+1}^{2n}\frac{1}{k}=\frac{1}{n+1}+\frac{1}{n+2}+\dots +\frac{1}{2n}>\frac{1}{2n}+\frac{1}{2n}+\dots +\frac{1}{2n}=n\frac{1}{2n}=\frac{1}{2}.$ Tehát $a_{2n}-a_n>\frac{1}{2}\forall n.$ Ezért $\epsilon =\frac{1}{2}$ esetén nem teljesül a Cauchy kritérium $\Rightarrow$ $(a_n)$ nem konvergens.

Összehasonlító kritérium ⁷

Majoráns kritérium

Tegyük fel, hogy $(a_n)$ [[#Nullsorozat [ 4|nullsorozat]], és $(b_a)$ olyan sorozat, melyre $|b_n|\le |a_n|\forall n\in \mathbb{N}$. ${\lim }_{n\to \infty }{b}_n=0$

Minoráns kritérium

Tegyük fel, hogy $(a_n)$ $\infty$-be divergál, vagyis ${\lim }_{n\to \infty }{b}_n=\infty$. Tegyük fel azt is, hogy van olyan $n$ index, melyre $b_n\ge a_{n}n\ge \mathbb{N}$. ${\lim }_{n\to \infty }{b}_n=\infty$

Abszolút konvergens sorok ⁸

$(\sum a_n)$ abszolút konvergens, ha: ${\sum }_{n=1}^{\infty }|a_n|<\infty .$

Feltételesen konvergens sorok ⁸

$(\sum a_n)$ végtelen sor feltételesen konvergens, ha [[#Konvergens [ 2|konvergens]], de nem [[#Abszolút konvergens sorok [ 8|abszolút konvergens]].

Hányadoskritérium ⁹

Tegyük fel, hogy $0<q<1$. $\left|\frac{a_{n+1}}{a_n}\right|\le q<1\forall n\in \mathbb{N}$ Ekkor a sor [[#Abszolút konvergens sorok [ 8|abszolút konvergens]]. $\left|\frac{a_{n+1}}{a_n}\right|\ge 1\forall n\in \mathbb{N}$ Ekkor a sor [[#Divergens [ 3|divergens]].

Gyökkritérium ¹⁰

Footnotes

1. Analízis 1. Jegyzet 46. oldal ↩

2. Analízis 1. Jegyzet 47. oldal ↩ ↩²

3. Analízis 1. Jegyzet 48. oldal ↩

4. Analízis 1. Jegyzet 35. oldal ↩

5. Analízis 1. Jegyzet 49. oldal ↩

6. Analízis 1. Jegyzet 37. oldal ↩ ↩²

7. Analízis 1. Jegyzet 37. oldal ↩

8. Analízis 1. Jegyzet 53. oldal ↩ ↩²

9. Analízis 1. Jegyzet 54. oldal ↩

10. Analízis 1. Jegyzet 57. oldal ↩