02 - Adatábrázolás és logikai áramkörök

Hozzátartózó előadás: Adatábrázolás és logikai áramkörök

Számrendszer átírása 10-es számrendszerre

Tízes számrendszer átírása más számrendszerre

Pl: 15 tízes számrendszerben átírása kettes számrendszerbe.

Szám	Maradék	Művelet
15	1 LSB (Least Significant Bit)	/ 2
7	1	/ 2
3	1	/ 2
1	1 MSB (Most Significant Bit)	/ 2
15 ⇒ 1111[2]

Pl: 27 tízes számrendszerben átírása kettes számrendszerbe.

Szám	Maradék	Művelet
27	1 LSB (Least Significant Bit)	/ 2
13	1	/ 2
6	0	/ 2
3	1	/ 2
1	1 MSB (Most Significant Bit)	/ 2
27 ⇒ 11011[2]

Pl: 27 tízes számrendszerben átírása nyolcas számrendszerbe.

Szám	Maradék	Művelet
27	3 LSB (Least Significant Bit)	/ 8
3	3 MSB (Most Significant Bit)	/ 8
27 ⇒ 33[8]

Pl: 27 tízes számrendszerben átírása tizenhatos számrendszerbe.

Szám	Maradék	Művelet
27	11 LSB (Least Significant Bit)	/ 16
1	1 MSB (Most Significant Bit)	/ 16
27 = 1B[16]

Shortcut

• Amennyiben az alap a kettes valahányadik hatványa

2-esből 8-asba shortcut

8 = 2 power 3

• Számjegyek csoportosítása hármasával, hátulról Pl: 11011 ⇒ 011, 011 ⇒ 33

2-esből 16-asba shortcut

8 = 2 power 4

• Számjegyek csoportosítása négyesével, hátulról Pl: 11011 ⇒ 0001, 1011 ⇒ 1B

Kifejezések

• bit: binary digit (0; 1)
• Byte: 8bit (00000000)
• Overflow (túlcsordulás): amikor egy műveletnél a kapott szám nem fér ki adott biten, a fennmaradó bit ami elveszik.

Info

byte < kilo < mega < giga < terra < peta

Warning

A ‘kibi’-k között a váltószám $1024$, míg a ‘kilo’-k között $1000$.

Warning

byte jelölése: $b$ Bit jelölése: $B$

Számok reprezentálása binárisan

Meg kell adni hogy:

• hány biten
• milyen kódolásban

Előjeles egész

• az első bit jelöli az előjelet Pl: 1111 = -7

Eltolásos egész

• jelölése: Excess -10 (-10el el van tolva) Pl: 0000 ⇒ 0 - 10 = -10 0001 ⇒ 1 - 10 = -9

Kettes komplemens ábrázolás

Ha a szám pozitív akkor kiírjuk kettesben, Ha negatív, 4 lépésben átalakítjuk:

• x = x + 1
• x = |x|
• binárissá alakítjuk
• minden számjegyet felcserélünk

Pl: 2 kettes komplemens ábrázolásban, 4 biten

Pozitív, tehát felírjuk binárisan: 2 % 2 = 0; 1 % 2 = 1; Tehát 2 ⇒ 0010[2]

Pl: -7-es komplemens ábrázolásban, 4 biten

Negatív, tehát először hozzáadunk egyet, abszolútértéket számolunk, felírjuk binárisan, majd számjegyeket cserélünk: -7 + 1 = -6 |-6| = 6 6 % 2 = 0; 3 % 2 = 1; 1 % 2 = 1; Tehát 6 = 0110[2] Felcseréljük a számjegyeket: 1001

Számok összeadása

Két bináris szám összeadása:

 1011[2] => 11
+1101[2] => 13
________
11000[2] => 24

Általános képlet két két bites szám összeadására:

A	B	Kimenet
0	0	0
1	0	1
0	1	1
1	1	0

• Ez a XOR vagyis az exklúzív vagy lagikai kapunak felel meg.
• Ha számolunk a túlcsordulással kell még más is.

Half adder

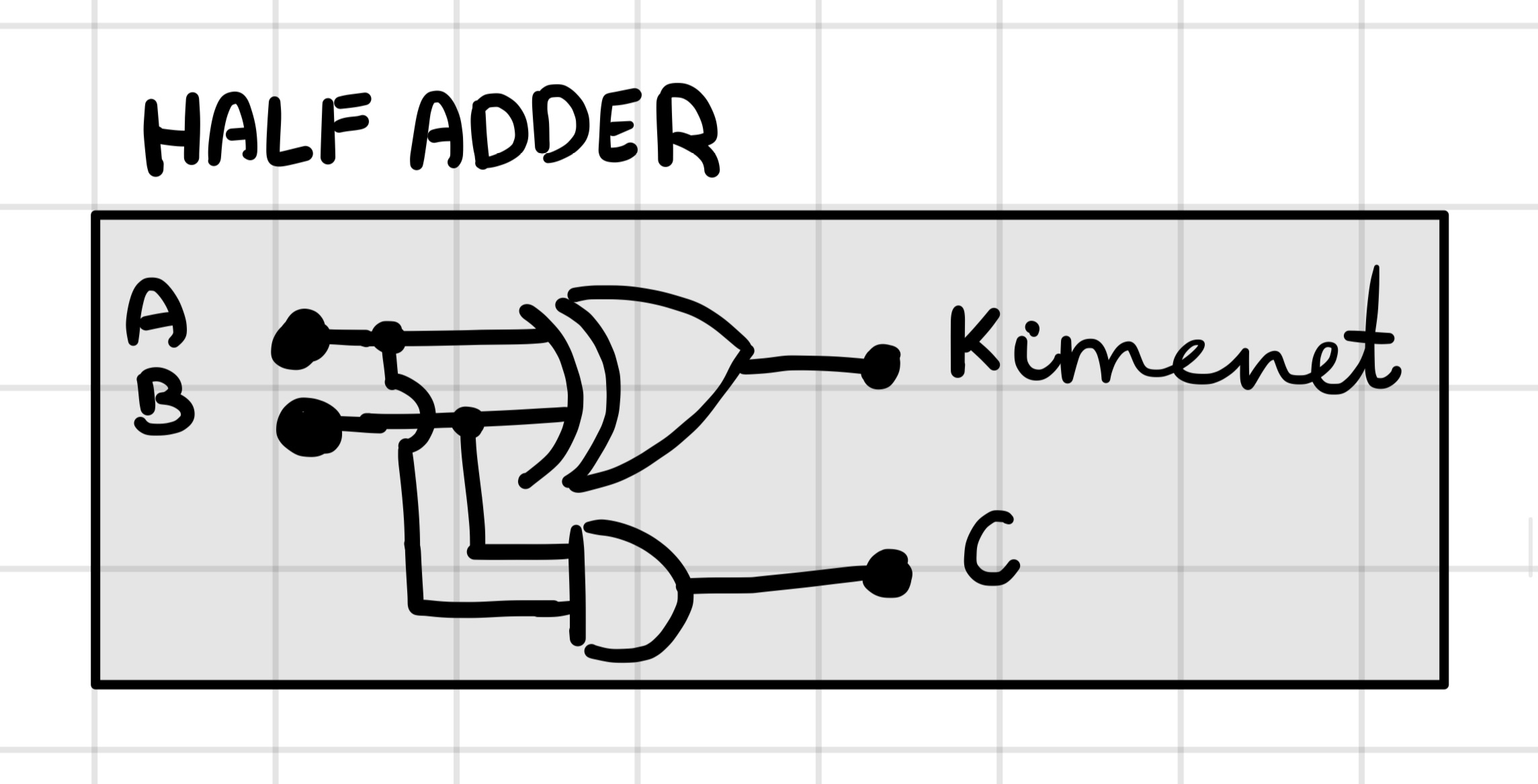
Full adder

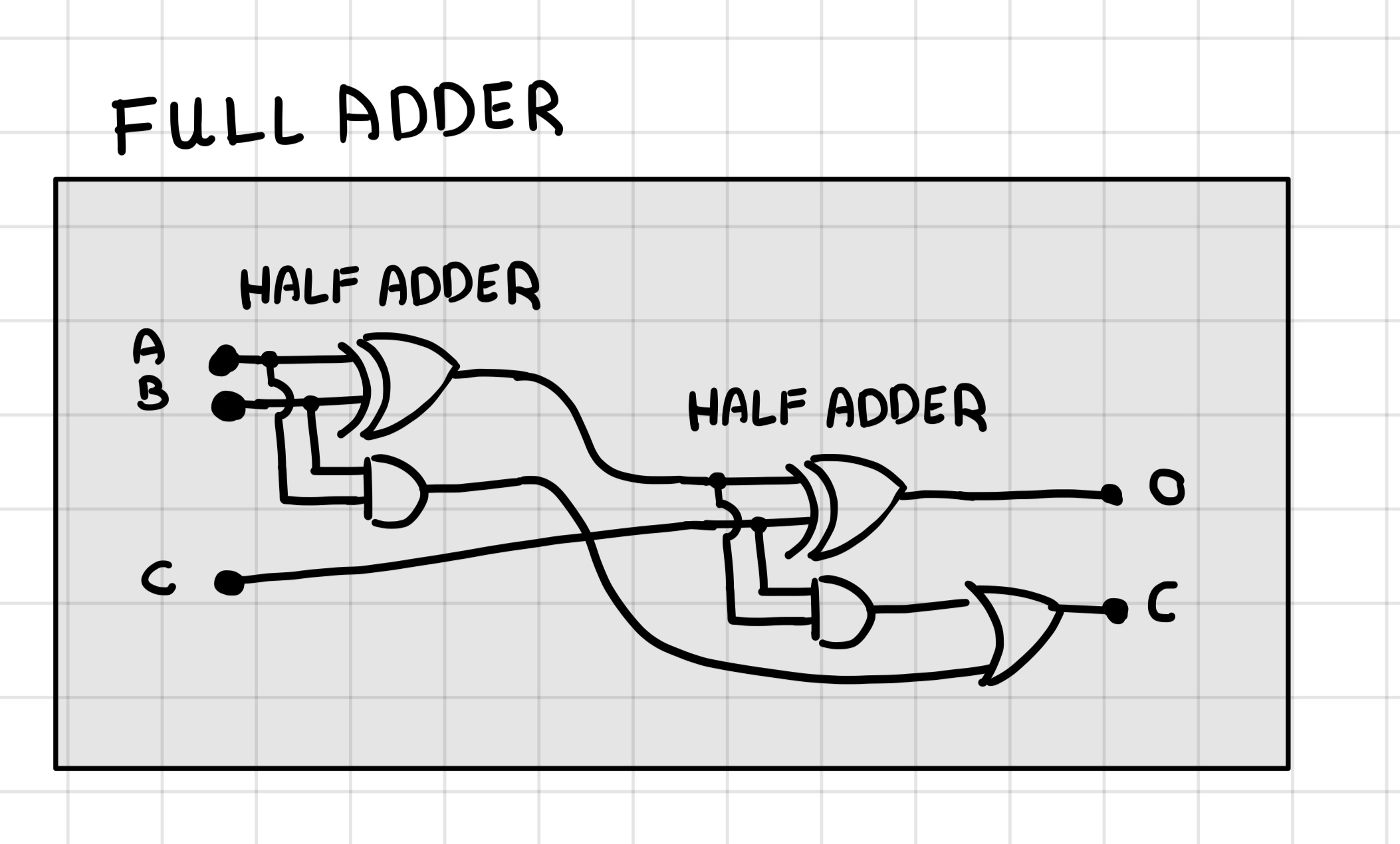
Számok kivonása

• ugyan úgy mint az összeadás, vagy
• összeadjuk a két számot, de a kivonandónak a kettes komplemensét vesszük

Szorgalmi

• full adder építés:
• kódolás kiderítés:
  1. UTF-8
  2. Windows 1252
  3. donno
  4. donno