06 - Függvények 4.

Szinusz függvény¹

Cosinus függvény¹

Érintő egyese

Legyen $x_0$ az $f$ függvény értelmezési tartományának belső pontja, itt differenciálható. Ekkor a függvény $x_0$ pontjához tartozó érintő egyenese $x_0\in D_f{y}_0=f(x_0)m=f^{\prime }(x_0)$ $y-y_0=m(x-x_0)\Rightarrow y=m(x-x_0)+y_0.$

Lokális szélsőértékek ²

Lokális minimum

Ha $x_0$-nak legalább egy környezete van, amelyre $f(x)\ge f(x_0)\forall x\in U\cap D_f.$

Lokális maximum

Ha $x_0$-nak legalább egy környezete van, amelyre $f(x_0)\ge f(x)\forall x\in U\cap D_f.$

Elégséges feltétel lokális szélsőértékre

Legyen $f:D_f\to R$, $x_0$-ban kétszer folytonosan differenciálható, és $f^{\prime }(x)=0$. Ekkor $f^{\prime \prime }(x_0)\ne 0$ esetén $x_0$-ban lokális szélsőérték van. Sőt, $f^{\prime \prime }(x_0)>0x_0\text{ lokaˊlis minimum}$ $f^{\prime \prime }(x_0)<0x_0\text{ lokaˊlis maximum}$

Info

Ha $f^{\prime \prime }(x)=0$, még nem eldönthető, vajon $x_0$-ban szélsőértéke van-e a függvénynek. (Innen az elégséges)

Szükséges feltétel lokális szélsőértékre

Legyen $f:D_f\to R$, $x_0$-ban differenciálható. Ekkor $f^{\prime }(x)=0.$

Globális szélsőértékek ³

Globális minimum

$f(x)\ge f(x_0)\forall x\in D_f$

Globális maximum

$f(x_0)\ge f(x)\forall x\in D_f$

Magasabb rendű deriváltak ⁴

Másodrendű derivált

Ha egy $f$ függvény deriválható $x_0$ egy környezetében, és ez az $f^{\prime }$ függvény deriválható $x_0$-ban, akkor ez az $f$ függvény másodrendű deriváltja. $f^{\prime \prime }(x)={\lim }_{x\to x_0}\frac{f^{\prime }(x)-f^{\prime }(x_0)}{x-x_0}$

N-ed rendű derivált

$\text{Jelo¨leˊse:}{f}^{(n)}(x)$

Stacionárius pont ³

Minden olyan $x_0\in D_f$ szám stacionárius pont amelynek derivált értéke $0$. $f^{\prime }(x_0)=0x_0\in D_f$

Középérték tételek ⁵

Rolle tétel

Legyen $f:[a,b]\to R$. Tegyük fel, hogy $f$

• folytonos $[a,b]$-n, és differenciálható $(a,b)$-n
• $f(a)=f(b)$ $\exists \epsilon \in (a,b)f^{\prime }(\epsilon )=0$ Másképpen: Ha egy függvény folytonos és differenciálható egy szakaszon, és két helyen is felveszi ugyan azt az értékét lesz $\epsilon$ pontja, ahol a deriváltja $0$ lesz ([[06 - Függvények 4.#Stacionárius pont [ 4]|Stacionárius pont]]).

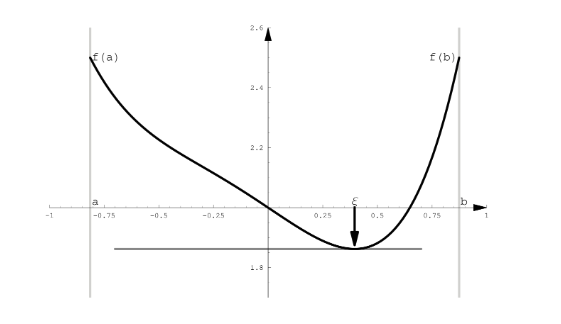
Lagrange-féle középérték tétel

Legyen $f:[a,b]\to R$. Tegyük fel, hogy $f$

• folytonos $[a,b]$-n, és
• differenciálható 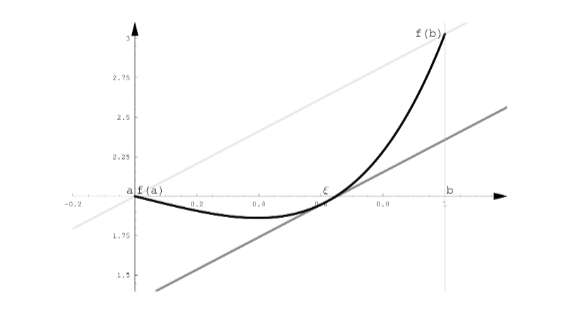$(a,b)$-n $\exists \epsilon \in (a,b)f^{\prime }(\epsilon )=\frac{f(b)-f(a)}{b-a}.$ Másképpen: Ha egy függvény folytonos és differenciálható egy szakaszon lesz olyan pont, ahol a ponthoz húzott érintő meredeksége megegyezik a szakasz két pontja között húzott szelő meredekségével.

Inverz függvény deriváltja ⁶

Tegyük fel, hogy $f$ szigorúan monoton, differenciálható függvény, melyre $f^{\prime }(x)\ne 0,x\in D_f$ mellett. Ekkor $f^{-1}$ is differenciálható, és $(f^{-1})(y)=\frac{1}{f^{\prime }(f^{-1}(y))}.$

Footnotes

1. Analízis 1. Jegyzet 68. oldal ↩ ↩²

2. Analízis 1. Jegyzet 117. oldal ↩

3. Analízis 1. Jegyzet 118. oldal ↩ ↩²

4. Analízis 1. Jegyzet 114. oldal ↩

5. Analízis 1. Jegyzet 119. oldal ↩

6. Analízis 1. Jegyzet 115. oldal ↩