05 - Függvények 3.

[[04 - Függvények 2.#Folytonosság [ 1]|Folytonosság]]

Szakadás ¹

Ha $f$ függvény az értelmezési tartomány egy $x_0$ pontjában nem folytonos, akkor ott szakadási helye van. Ezen kívül $x_0\notin D_f$, akkor is szakadási hely, ha $(x_0-\delta ,x_0+\delta )\backslash \{x_0\}\subset D_f\delta >0.$ Vagyis: Ha egy $x_0$ környezetében, amiből kivesszük az $x_0$-t, eleme a függvény [[03 - Számsorozatok 2. és Függvények 1.#Értékkészlet [ 4]|értékkészlet]]ének akkor szakadási pont.

Osztályozásuk:

• Elsőfajú szakadás

  $x_0$-ban elsőfajú szakadás van, ha létezik a függvénynek az $x_0$-ba tartó baloldali, és jobboldali határértékei és ezek kisebbek, mint végtelen. Megszüntethető szakadás, ha a két oldalsó szélsőérték megegyezik, és ${\lim }_{x\to x_0}f(x)\ne f(x).$

• Másodfajú szakadás

  Ha nem elsőfajú.

Bolzano tétel ²

Adott $f:[a,b]\to \mathbb{R}$ folytonos függvény. Tegyük fel, hogy $f(a)<0<f(b)$. Ekkor $\exists \text{upzeta}\in (a,b)$ , ahol $f(\text{upzeta})=0$.

Másképpen: Ha van egy folytonos zárt függvényem, aminek az egyik vége negatív, a másik pozitív, akkor biztosan lesz olyan pontja amely nulla.

Bizonyítás

Meghatározunk egy alkalmas $\text{upzeta}$ pontot.

1. Legyen $a_1=a$ és $b_1=b$.
2. Legyen ${\text{upzeta}}_1=\frac{a_1+b_1}{2}$. Ha $f({\text{upzeta}}_1)=0$ akkor készen vagyunk.

• Ha $f({\text{upzeta}}_1)>0$ akkor legyen $a_2=a_1$, $b_2=c_1$.
• Ha $f({\text{upzeta}}_1)<0$ akkor legyen $a_2=c_1$, $b_2=b_1$ Ekkor $f(a_2)<0f(b_2)>0$

3. Ha $f({\text{upzeta}}_1)\ne 0$ újra próbálkozunk Végül két eset következhet be
4. véges sok lépésben vége van az iterációnak és megkapjuk a kívánt $\text{upzeta}$ pontot.
5. Nincs vége az iterációnak, ekkor az intervallumok végpontjaiból álló sorozatokra teljesül, hogy:

• $(a_n):f(a_n)<0$
• $(b_n):f(b_n)>0$

Következménye

Tegyük fel, hogy $f$ folytonos az $[a,b]$ intervallumban. $f(a)<f(b)$. Ha $c$ tetszőleges szám, melyre: $f(a)<c<f(b)$, akkor létezik olyan $\text{upzeta}\in (a,b)$, melyre $f(\text{upzeta})=c$.

Inverz függvény folytonossága ²

Adott $f$ függvény, amely $f:[a,b]\to \mathbb{R}$, szigorúan monoton növekvő, folytonos. $c\in [f(a),f(b)]\mathcal{E}\in [a,b]$ Az inverz függvény a $c\to \mathcal{E}$ leképezés.

Weierstrass I. tétele ³

Legyen $f:[a,b]\to \mathbb{R}$ függvény folytonos.

Ekkor az $f$ függvény korlátos.

Weierstrass II. tétele ³

Legyen $f:[a,b]\to \mathbb{R}$ függvény folytonos.

Ekkor az $f$ függvény felveszi a minimumát és a maximumát $[a,b]$-ben.

Nevezetes határértékek ⁴

${\lim }_{x\to 0}\frac{\sin x}{x}=1$ ${\lim }_{x\to 0}\frac{1-\cos x}{x^2}=\frac{1}{2}$ ${\lim }_{x\to \infty }{x}^{\frac{1}{x}}=1\text{Mert:}$ $x^{\frac{1}{x}}=\sqrt[x]{x}$

Differenciálszámítás

Differenciahányados ⁵

Adott $f$ függvény, és $x_0\in \text{int}D$. Az $x$ ponthoz tartozó differenciálhányados a szelő meredeksége. $\frac{f(x)-f(x_0)}{x-x_0},x\in D_f$

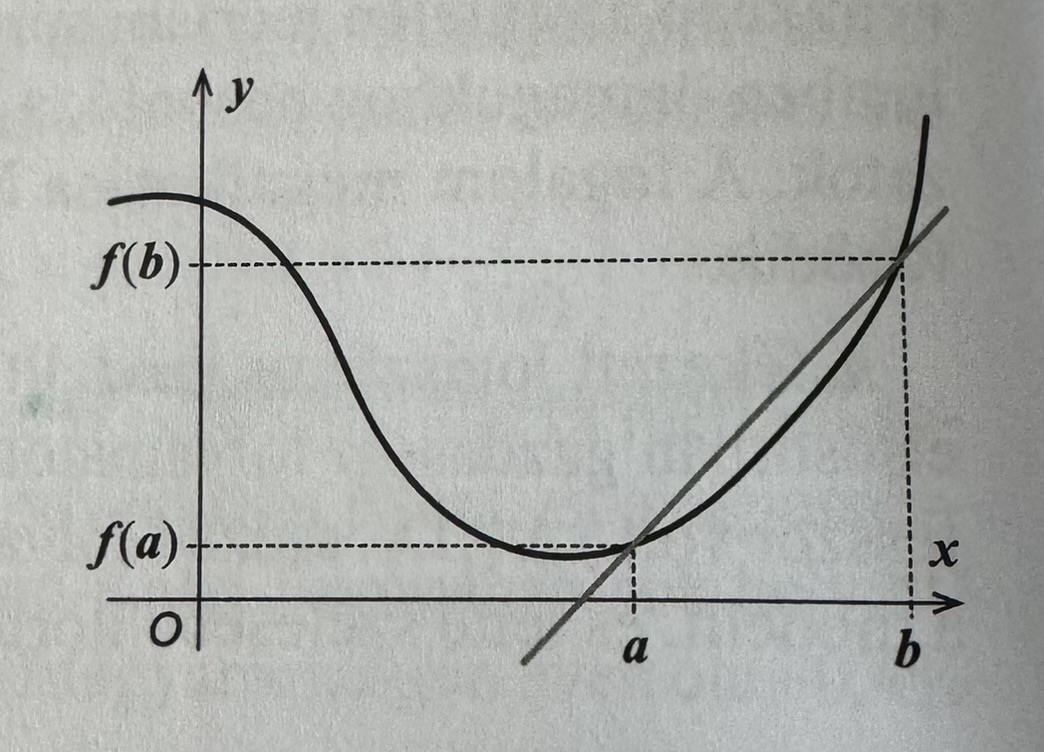
Derivált

A differenciálhányados határértéke a derivált. $f(x{)}^{\prime }={\lim }_{x\to x_0}\frac{f(x)-f(x_0)}{x-x_0}=\frac{df}{dx}(x_0)$

Deriválási szabályok

$(f+g{)}^{\prime }(x_0)=f^{\prime }(x_0)+g^{\prime }(x_0)$ $(f\cdot g{)}^{\prime }(x_0)=f^{\prime }(x_0)\cdot g(x_0)+f(x_0)\cdot g^{\prime }(x_0)$

Footnotes

1. Analízis 1. Jegyzet 85. oldal ↩

2. Analízis 1. Jegyzet 89. oldal ↩ ↩²

3. Analízis 1. Jegyzet 94. oldal ↩ ↩²

4. Analízis 1. Jegyzet 95. oldal ↩

5. Analízis 1. Jegyzet 104. oldal ↩